[기타 공부] Hough Transform

OpenCV에서 Canny detection으로 얻은 edge들을 Hough transform을 사용하여 직선을 검출했던 기억이 있다. 사용하면서도 그 원리를 알아보지 않았는데, 이번에는 그 원리를 자세하게 공부해보았다.

 

 

 

Hough transform의 필요성

Hough transform은 1960년대 제안된 알고리즘이다. 당시 gradient를 기반으로 edge를 detect하는 방법은 한계가 존재하였다.

위와 같은 자전거 이미지와 여기서 구한 edge가 있다고 생각해보자. 원형의 모양을 가지는 두 바퀴를 찾는것을 목표로 하고 있다. 하지만 기존의 edge에서는 어려움이 존재한다.

1. Data의 어떤 부분을 circle로 학습해야하는가
2. 원하는 circle의 edge가 불완전하게 존재한다는 점
3. 원하는 edge들 이외에도 다른 부분의 edge가 겹치며 noise가 존재한다는 점

이 3가지 문제를 한 번에 해결하기위해 Hough transform이 고안되었다.

 

 

 

Hough transform (Line detection)

Hough transform 중에서 먼저 line detection을 살펴보자. 이것을 이해하기 위해서는 좌표계를 생각해야한다. 2차원 좌표계라고 했을 때 우리는 xy 좌표계를 떠올릴 것이다. 그 위에 존재하는 직선은 아래와 같이 나타낼 수 있다.

Hough transform은 이러한 직선을 parameter space에서 바라보는 관점으로 시작한다. 즉, y와 x를 변수로 바라보던 위의 식을 slope를 의미하는 a와 intercept를 의미하는 b의 식으로 바꾸는 것이다.

즉 기존 xy space에서 y=ax+b라는 식이 x0, y0라는 특정 점을 가진다는 것을 알게 되면, parameter space에서는 -x0가 기울기가 되고 y가 절편이 되는 것이다. 그렇다면 xy space에서의 직선은 parameter space에서 어떻게 표현될까.

 

xy space에서 하나의 점은 parameter space에서 하나의 직선으로 표현된다는 것을 알았다. xy space에서의 직선은 이들의 m과(기울기) c가(절편) 동일하다는 것을 의미한다. 따라서 parameter space로 넘어가면 여러 직선이 하나의 교점을 갖는 형태로 나타난다. 바로 이것이 직선이 parameter space에서 표현되는 방법이다.

 

Hough transform의 주요 아이디어는 위의 방식을 기반으로 한다. 예를 들어, 이미지의 edge를 검출하고 이것을 parameter space로 변환한 뒤 직선들이 많이 교차되는 지점을 찾아서 직선을 검출하는 것이다. 이것을 알고리즘으로 구현하기 위해서 축적 배열(Accumulation array)를 적용시켰다.

 

직선을 arra 형태로 표현하고, 겹치는 부분은 정수를 통해 겹치는 직선의 수를 표현하는 방법이다. 하지만 xy space를 바로 parameter space로 변환하여 사용했을 때 몇 가지 문제가 존재한다.

1. m의 범위에 제한이 없기 때문에, 처리해야하는 양에 따라서 매우 큰 accumulator가 필요해지고, 계산과 memory의 소모가 커진다.
2. y축에 평행한 직선이라면 m이 무한대가 되는데, parameter space에서는 표현이 불가능하다.

따라서 세타와 ρ로 좌표를 표현하는 좌표계를 사용한다. 세타는 직선과 x축 사이의 각도, ρ는 직선과 원점 사이의 수직 거리를 의미한다.

극좌표계를 사용하는 이유는 유한성을 통해 기존 xy space를 사용할 때 마주했던 문제들을 해결하기 위해서이다..

1. 세타의 범위가 유한해진다는점, 0~pi
2. 거리 ρ가 이미지 사이즈를 넘을 수 없기 때문에 유한한 범위라는 점

이것을 parameter space로 표현하면 sinusoidal한 함수로 나타난다. 그리고 마찬가지로 많은 sinusoial 함수가 교차하는 지점을 찾는 것으로 직선 검출을 수행한다.

 

 

 

Hough transform (Circle detection)

이와 비슷한 방법으로 원을 검출할 수 있다. 원의 방정식은 아래와 같다.

 

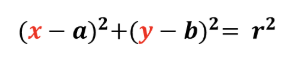
xy space에서 원 위의 한 점은 parameter space에서 어떻게 표현이 될까? 식으로 표현해보면 아래와 같고 이것 또한 원이 되는 것을 알 수 있다. 즉 a, b, r을 변수로 가지는 3차원 공간에 표현해야한다.

 

한 번에 생각하면 복잡해지니 먼저 a,b만 변수로 생각해보자. 한개의 점만을 표현한다면 다음과 같이 하나의 원으로 나타날 것이다.

 

원 위의 여러 점을 표현한다면 다음과 같이 여러 원이 나타나고, 이들은 1개의 교점을 갖게 될 것이다.

 

최종적으로 r에 연속적인 값을 대입하며 3차원 공간 상에 표현하면 원뿔형태의 도형이 만들어지고 여기서도 한 개의 교점을 가지게 된다.

 

하지만 이렇게 3차원까지 차원을 확장하여 많은 원뿔이 교차하는 지점을 찾는 방법은 많은 메모리와 연산량을 필요로한다. 따라서 원의 검출을 위해서는 Hough gradient라는 방법이 사용된다. 이것은 gradient를 통해 원의 중심을 찾고, 적절한 반지름을 구하는 방법이다. 어떻게 gradient로 원의 중심을 구할 수 있을까.

 

Canny detection에서 edge와 gradient는 직교한다는 특성을 살펴보았다. 원에서도 마찬가지이다. 여기서는 원의 접선을 떠올리면 이해가 편하다. 우리는 원의 edge 정보에서 원 위의 각 점에대한 gradient를 구한다. 아래 사진에서 빨간색 방향이 gradient이다. 이는 자연스럽게 중심을 향하고 이와 수직인 방향의 벡터가 경계면을 나타낸다.

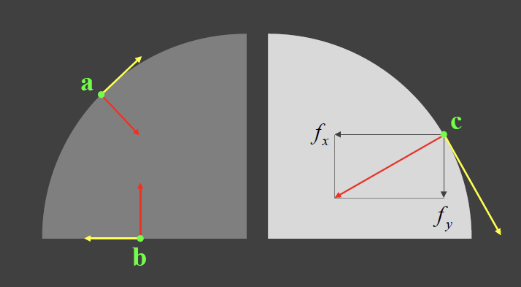
가지고 있는 원의 edge 정보에 대해서 이런식으로 여러 점으로 gradient 방향 직선을 그어주고, 교차하는 직선의 수가 임계값을 넘어가면 해당 교점을 원의 중심으로 정의한다. 이후 반지름을 조절해가며 edge pixel이 충분히 존재하는지 확인하며 원을 검출해내는 방식이다.

 

 

 

참고: https://developer-lionhong.tistory.com/29

참고: https://www.youtube.com/watch?v=XRBc_xkZREg